杜鹃声

斜阳暮

误差反向传播法

发表于 更新于

误差反向传播法是一种能高效计算权重参数梯度的方法。要理解它一般有两种方法，一种是基于数学式，另一种是基于计算图（computational graph）。接下来会补充讲解计算图的理解方法。

计算图

计算图会将计算过程用图表现出来。这里的图形是数据结构图，通过多个节点和边来表示。

计算图通过节点和箭头表示计算过程，节点用 ⚪ 表示，⚪ 中是计算的内容。将计算的结果写在箭头的上方，表示各个节点的计算结果从左到右传递。计算时就像电流从左到右流动，计算结果从左向右传递。到达最右边的计算结果后，计算过程就结束了。

使用计算图计算的流程一般是

  1. 构建计算图
  2. 在计算图上从左到右计算

这里的“从左到右”传播被称为正向传播（forward propagation），后面我们还会遇见反向传播（backward propagation）

计算图的特征之一是通过“局部计算”来获得最终结果，无论全局发生了什么，都只能根据和自己相关的信息来输出结果。在计算图的全局来看，这就像是工厂的流水线，每个工人所承担的都是简化过的工作，将每项工人的成果传递给下一个工人就可完成整个任务。计算图就是通过传递每个局部计算的计算结果得到的全局复杂计算的结果。

并且，通过反向传播可以高效计算导数。

链式法则

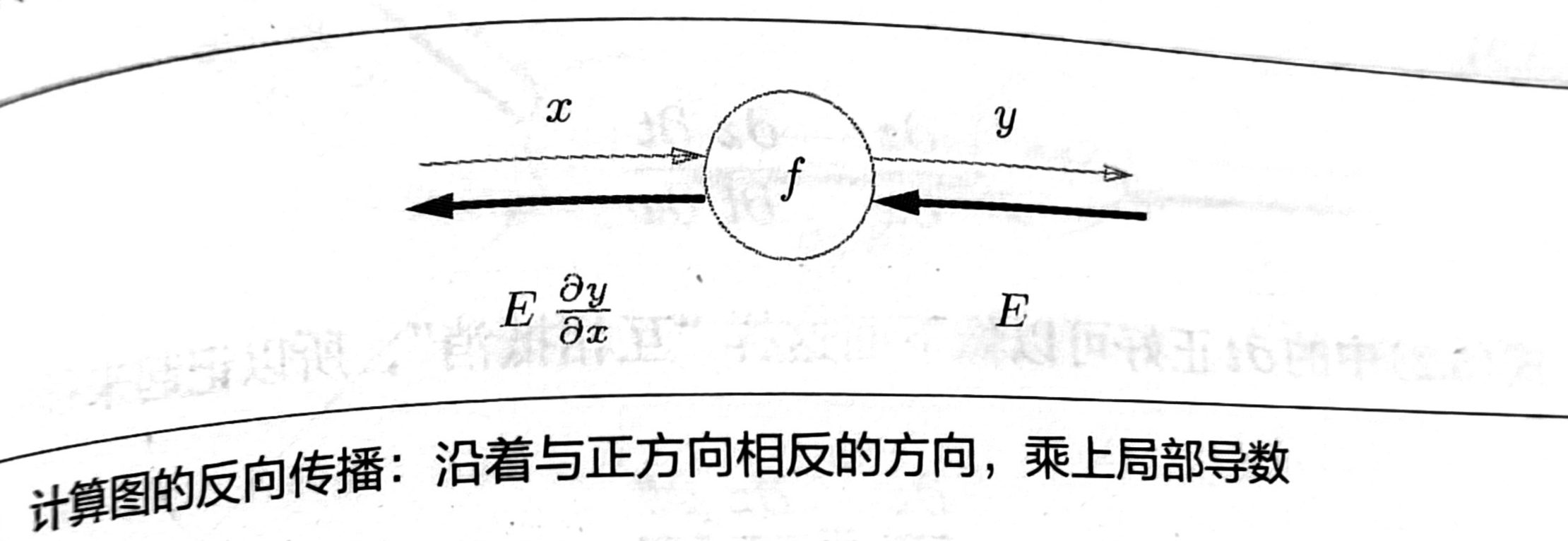
反向传播会将局部导数向正方向的反方向（从右到左）传递，传递这个局部导数的原理是基于链式法则（chain rule）的。下面是关于链式法则的解释。

假设存在 y = f(x)的计算，这个计算的反向传播如图所示：

IMG_20240717_215331

在反向传播里，加法的是将上游的值赋予下游的值；乘法的则为 \(\frac{\partial z}{\partial x} \,+ \,y\) 或者\(\frac{\partial z}{\partial y} \,+ \,x\)

简单层的实现

接下来我们将会把实现的计算图的乘法节点称为“乘法层”（Mullayer）,加法节点称作“加法层”（Addlayer）。习惯上，我们会把实现神经网络的“层”实现为一个类，这里的“层”指的是神经网络中功能的单位。如负责sigmoid函数的Sigmoid，负责矩阵乘积的Affine等。

乘法层会初始化x和y来保存正向传播时的输入。backward()方法会将上游传下来的导数乘正向传播的翻转值，然后传给下游。

加法层不需要刻意进行初始化。其中的forward（）方法会接受两个参数相加后输出，backward（）方法则会将上游传下的导数原封不动输出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Mullayer:
    def __init__(self) -> None:
        self.x = None
        self.y = None

    def forward(self, x, y):
        self.x = x
        self.y = y
        out = x * y

        return out
    

    def backward(self, dout):
        dx = dout * self.y
        dy = dout * self.x

        return dx, dy
    
class Addlayer:
    def __init__(self) -> None:
        pass

    def forward(self,x,y):
        out = x + y
        
        return out
    
    def backward(self,x,y,dout):
        dx = dout *1
        dy = dout *1
        
        return dx,dy

激活函数层的实现

激活函数ReLU(Rectified Linear Unit),如下式： \[ \text{ReLU}(x) = \begin{cases} 0 & \text{if } x < 0 \\ x & \text{if } x \geq 0 \end{cases} \] 求出导数为（假如是x）： \[ \frac{\partial f}{\partial x} = \begin{cases} 0 & \text{if } x < 0 \\ 1 & \text{if } x \geq 0 \end{cases} \] 在神经网络层的实现中，一般假定forward()和backward()的参数是NumPy数组。

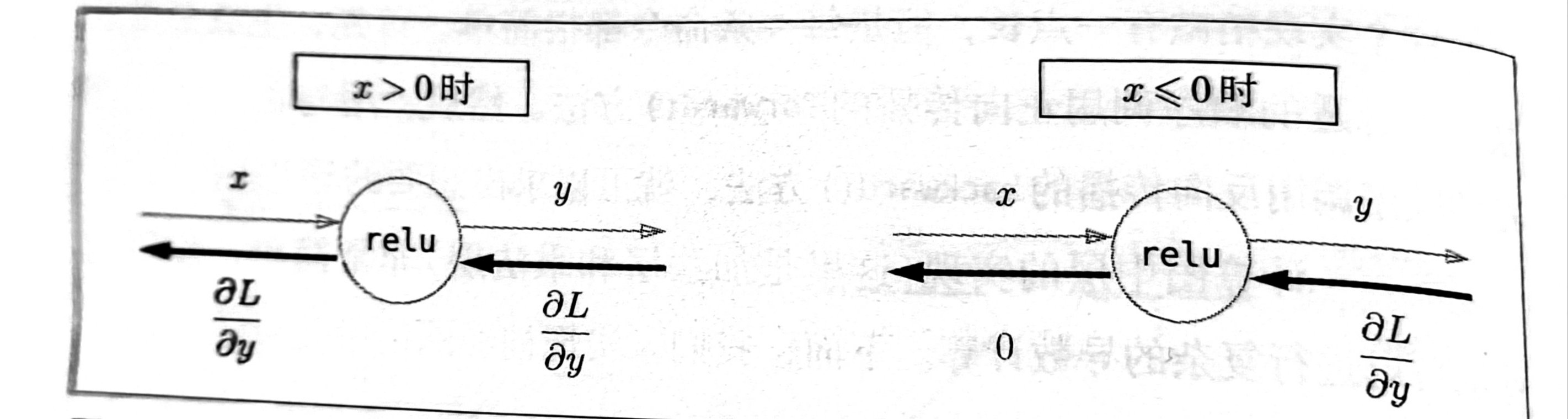
ReLU函数的作用就像电路中的开关，正向传播时，假如有电流通过，那就把开关设为on，否则设为off;当反向传播时，开关为on电流会直接通过，反之为off时就不会有任何电流通过。

激活函数Sigmoid如下： \[ \sigma(x) = \frac{1}{1 + e^{-x}} \] 正向传播时输出保存在了实例变量out中，反向传播时使用该变量out进行计算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import numpy as np



class ReLu:
    def __init__(self) -> None:
        self.mask = None

    def forward(self,x):
        self.mask = (x <=0 )
        out = x.copy()
        out[self.mask] = 0

        return out
    
    def backward(self,dout):
        dout[self.mask] = 0
        dx = dout

        return dx
    


class Sigmoid:
    def __init__(self):
        self.out = None

    def forward(self, x):
        out = 1 / (1 + np.exp(-x))
        self.out = out
        return out

    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out

        return dx

附上ReLu和Sigmoid的计算图

IMG_20240717_232529
IMG_20240717_232516

Affine/Softmax层的实现

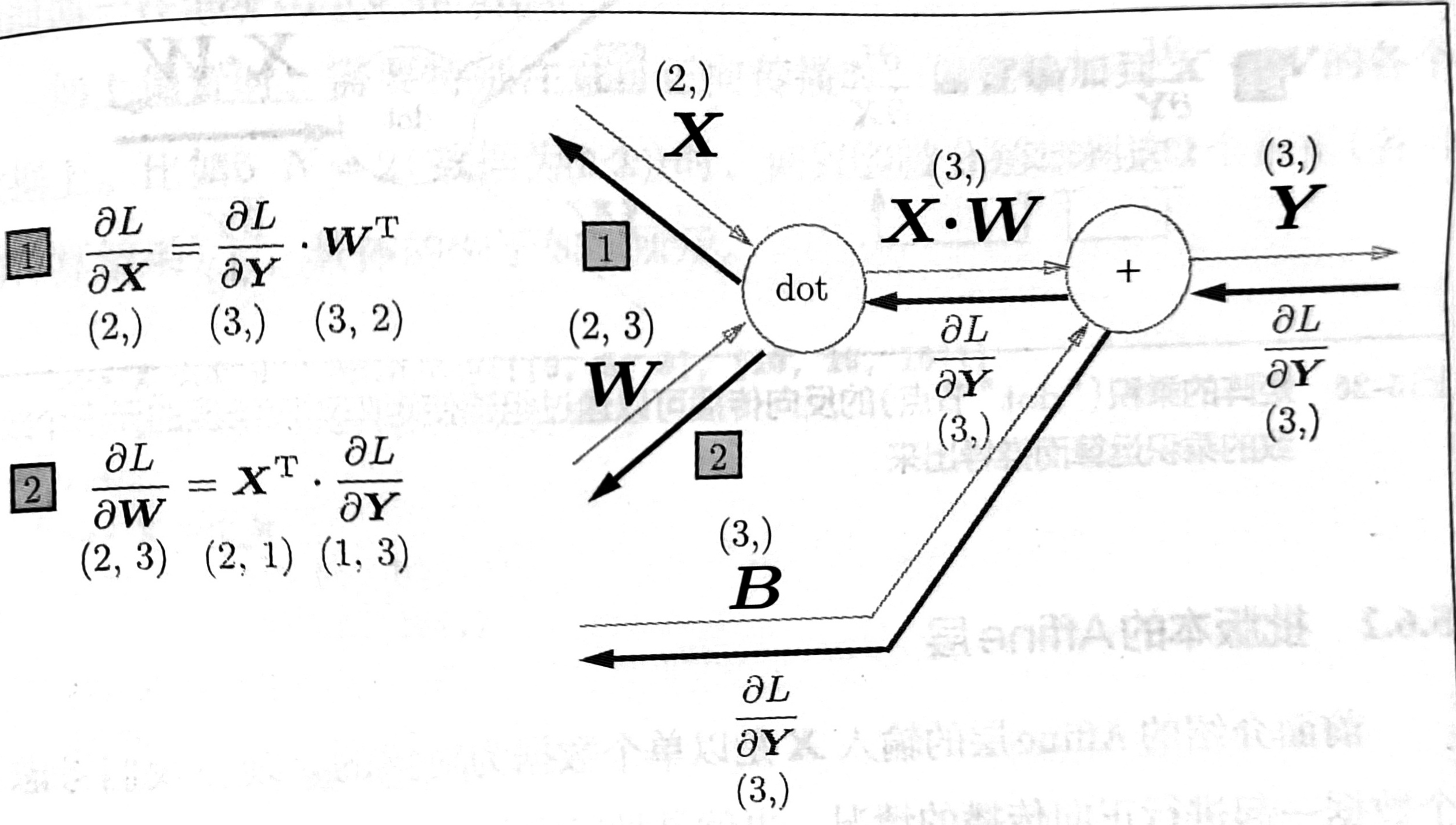
神经网络的正向传播中，为了计算加权信号的总和，使用了乘积运算。

IMG_20240717_233625

当输入X为单个变量的计算图。

当N个数据一起输入时计算图变为：

IMG_20240717_233909 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Affine:
    def __init__(self, W, b):
       self.w = W
       self.b = b
       self.x = None
       self.dw = None
       self.db = None

    def forward(self, x):
        self.x = x 
        out = np.dot(x, self.w) + self.b

        return out
    
    def backward(self, dout):
        dx = np.dot(dout, self.w.T)
        self.dw = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)

        return dx

Softmax-with-Loss层

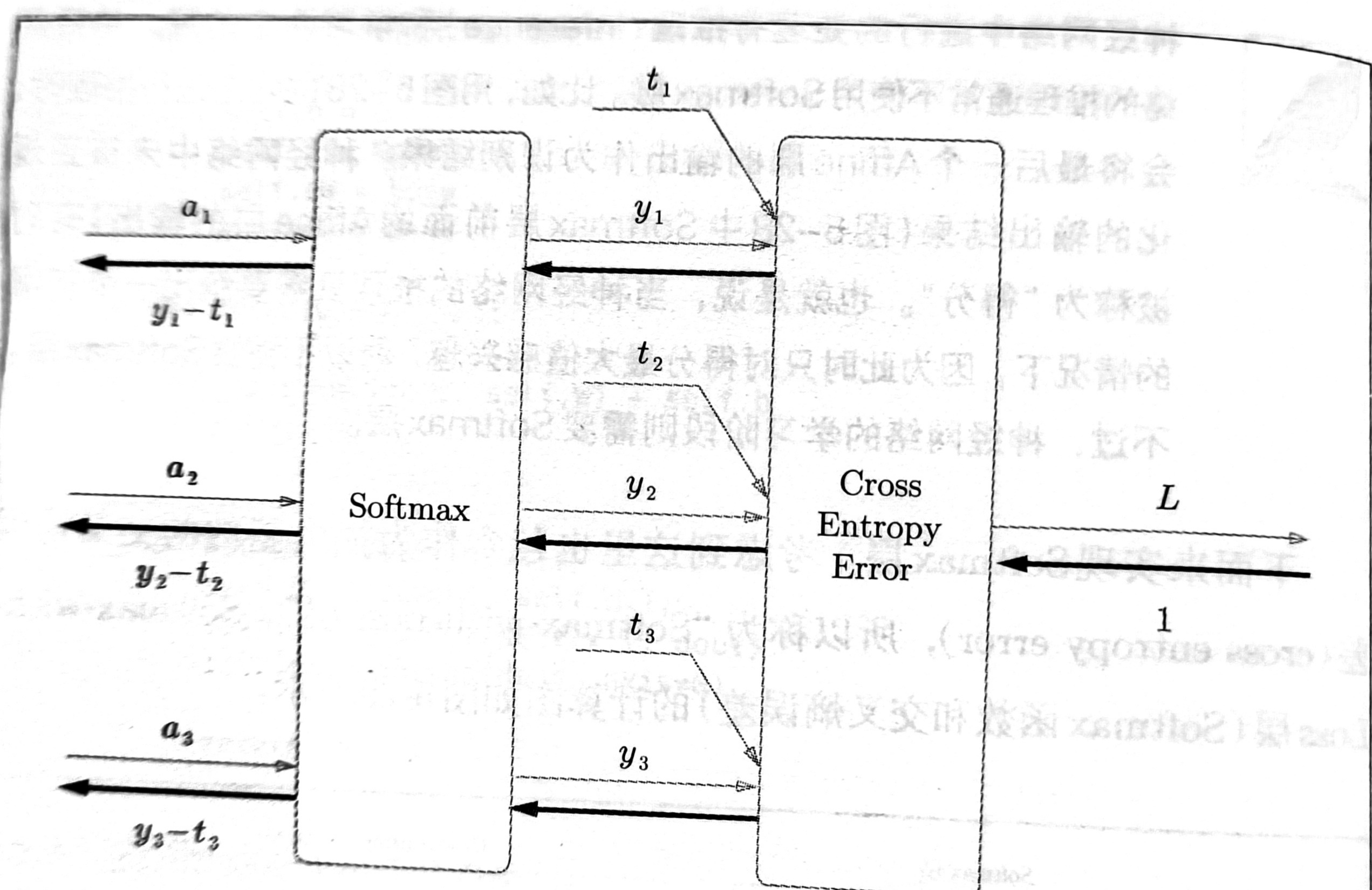
softmax函数会将输入全部正规化后输出。由于这里也包含作为损失函数的交叉熵误差（cross entropy error），所以称为"Softmax-with-Loss"层。softmax层的计算图有些复杂，这里给出一个简化版的：

IMG_20240717_234920

图中要注意的是反向传播的结果。Softmax层的反向传播得到了(y_1-t_1,y_2-t_2,y_3-t_3)这样“漂亮”的结果。由于（y_1，y_2，y_3）是Softmax层的出、（t_1，t2,t_3)是监督数据，所以（y_1-t_1，y_2-t_2，y_3-t_3）是Softmax层的输出和监督标签的差分。神经网络的反向传播会把这个差分表示的误差传递给前面的层，这是神经网络学习中的重要性质。 神经网络学习的目的就是通过调整权重参数，使神经网络的输出（Softmax的输出）接近监督标签。因此，必须将神经网络的输出与监督标签的误差高效地传递给前面的层。刚刚的(y_1-t_1,y_2-t_2,y_3-t_3)正是Softmax层的输出与监督标签的差，直截了当地表示了当前神经网络的输出与监督标签的误差。 这里考虑一个具体的例子，比如思考监督标签是（0,1,0)，Softmax层的输出是（0.3,0.2,0.5)的情形。因为正确解标签处的概率是0.2（20%），这个时候的神经网络未能进行正确的识别。此时，Softmax层的反向传播传递的是（0.3,-0.8,0.5)这样一个大的误差。因为这个大的误差会向前面的层传播，所以Softmax层前面的层会从这个大的误差中学习到“大”的内容。

以下是层的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None
        self.y = None # softmax的输出
        self.t = None # 监督数据

    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)
        
        return self.loss

    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        if self.t.size == self.y.size: # 监督数据是one-hot-vector的情况
            dx = (self.y - self.t) / batch_size
        else:
            dx = self.y.copy()
            dx[np.arange(batch_size), self.t] -= 1
            dx = dx / batch_size
        
        return dx

误差反向传播法的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
import sys, os
sys.path.append("E:\\Deep_learn\\ORIGAINAL")
import numpy as np
from common.layers import *
from common.gradient import numerical_gradient
from collections import OrderedDict


class TwoLayerNet:

    def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01):
        # 初始化权重
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size) 
        self.params['b2'] = np.zeros(output_size)

        # 生成层
        self.layers = OrderedDict()
        self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
        self.layers['Relu1'] = Relu()
        self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])

        self.lastLayer = SoftmaxWithLoss()
        
    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)
        
        return x
        
    # x:输入数据, t:监督数据
    def loss(self, x, t):
        y = self.predict(x)
        return self.lastLayer.forward(y, t)
    
    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        if t.ndim != 1 : t = np.argmax(t, axis=1)
        
        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy
        
    # x:输入数据, t:监督数据
    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)
        
        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
        
        return grads
        
    def gradient(self, x, t):
        # forward
        self.loss(x, t)

        # backward
        dout = 1
        dout = self.lastLayer.backward(dout)
        
        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        # 设定
        grads = {}
        grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
        grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db

        return grads

通过将神经网络的组成元素用层的方式实现，可以轻松的构建不同的神经网络。

由于数值微分的实现简单，所以一般用数值微分来比较误差反向传播法的结果来验证误差反向传播法的实现是否正确。这个操作被称作梯度确认。

欢迎关注我的其它发布渠道